OPTIMAL TENSOR TRANSPORT - AAAI’22
A new article by the Laboratoire Hubert Curien’s Data Intelligence Team will be presented during the next AAAI Conference on Artificial Intelligence (22nd February - 1st March 2022).
The optimal transport problem has recently found many applications at the core of machine learning, and especially in transfer learning. Tanguy Kerdoncuff’s latest contribution to this subject, presented in his Ph. D. thesis, generalizes and unifies several existing formulations of optimal transport. The published article therefore explores a unified formulation, Optimal Tensor Transport (OTT), that includes a scalable stochastic optimization algorithm with convergence guarantees. This formulation also opens a whole range of new applications where datasets have more complex structures.
This paper is part of the TADALoT Project funded by the region Auvergne-Rhône-Alpes (France) with the Pack Ambition Recherche (2017, 17 011047 01).
Abstract
Optimal Transport (OT) has become a popular tool in machine learning to align finite datasets typically lying in the same vector space. To expand the range of possible applications, Co-Optimal Transport (Co-OT) jointly estimates two distinct transport plans, one for the rows (points) and one for the columns (features), to match two data matrices that might use different features. On the other hand, Gromov Wasserstein (GW) looks for a single transport plan from two pairwise intra-domain distance matrices. Both Co-OT and GW can be seen as specific extensions of OT to more complex data. In this paper, we propose a unified framework, called Optimal Tensor Transport (OTT), which takes the form of a generic formulation that encompasses OT, GW and CoOT and can handle tensors of any order by learning possibly multiple transport plans. We derive theoretical results for the resulting new distance and present an efficient way for computing it. We further illustrate the interest of such a formulation in Domain Adaptation and Comparison-based Clustering.
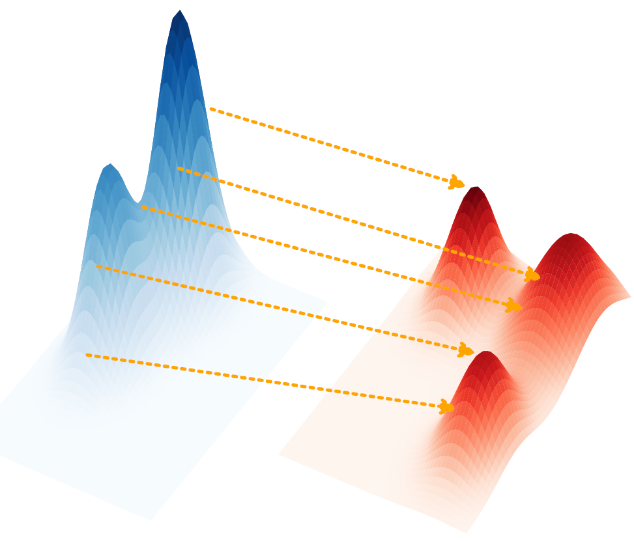
The traditional optimal transport problem, here illustrated in 2D: the goal is to find the optimal transport plan (in orange) to reshape the blue mass into the red one. This optimal transport problem corresponds to OTT1 with F=2
Illustration : The traditional optimal transport problem, here illustrated in 2D: the goal is to find the optimal transport plan (in orange) to reshape the blue mass into the red one. This optimal transport problem corresponds to OTT1 with F=2
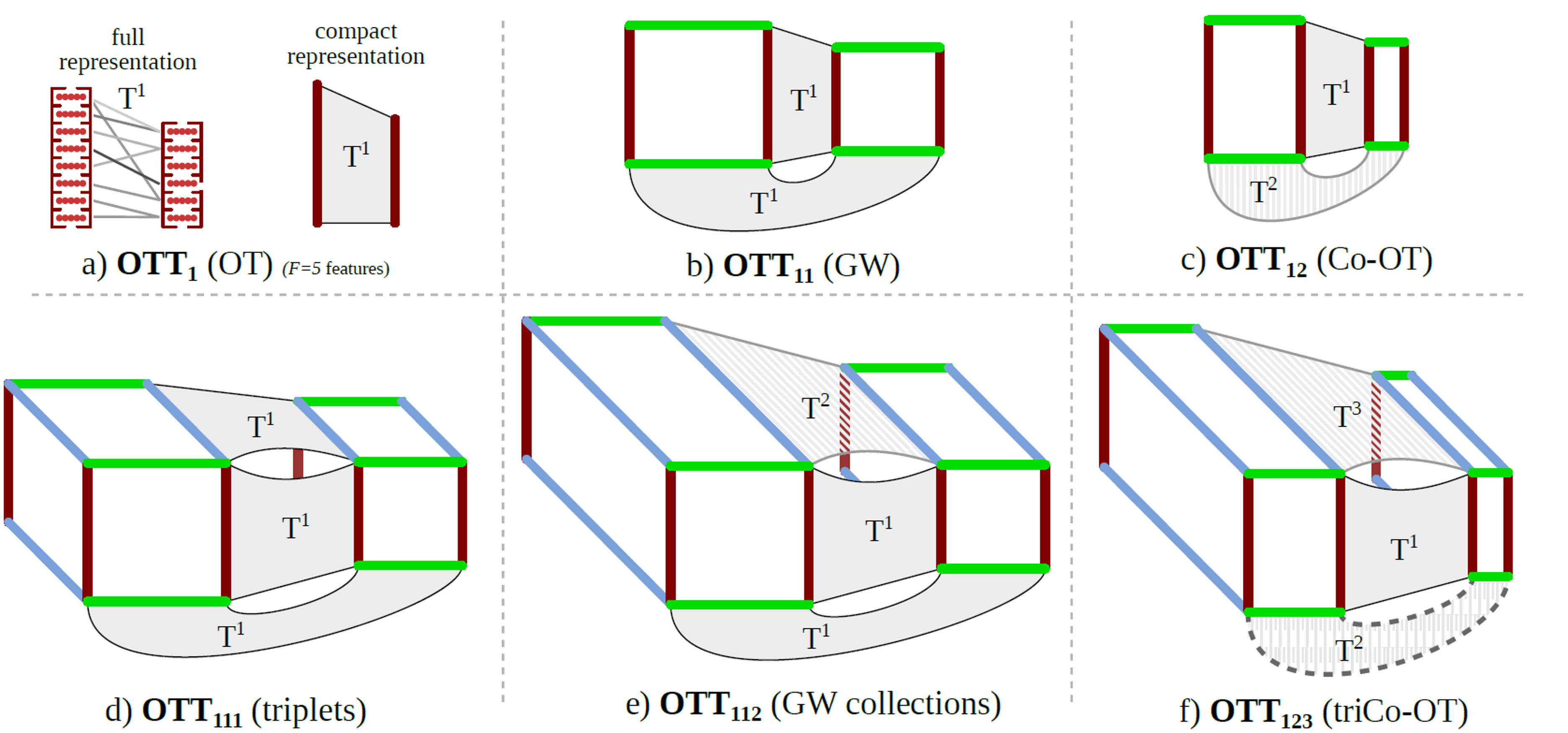
Optimal Tensor Transport (OTT): 1st row: reformulation of 3 existing optimal transport formulations, 2nd row: some novel formulations, falling into the OTT generalization
Illustration above: Optimal Tensor Transport (OTT):
- 1st row: reformulation of 3 existing optimal transport formulations,
- 2nd row: some novel formulations, falling into the OTT generalization.
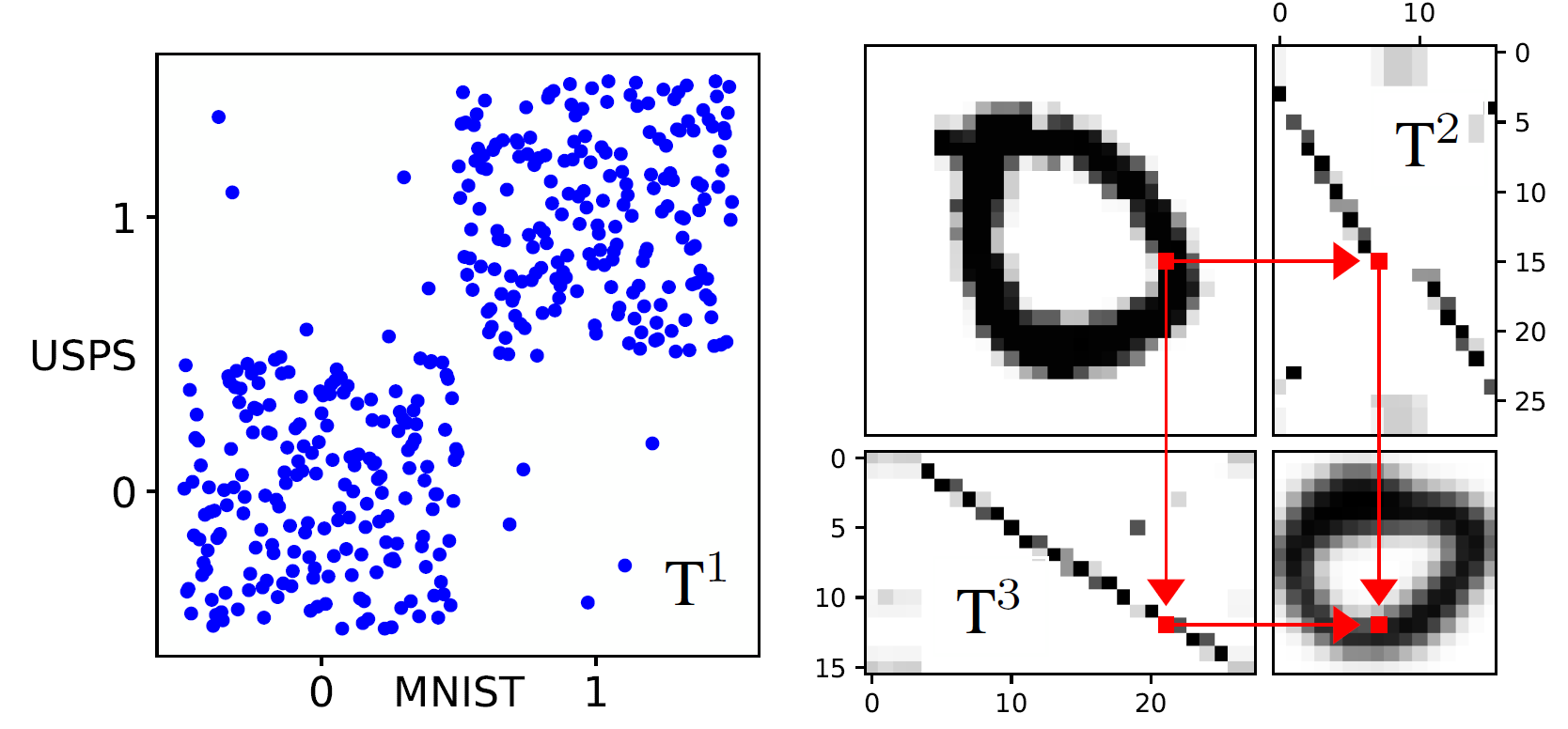
(Left) Transport plan T 1 between 400 images (only digits 0 and 1) of MNIST and USPS datasets; (Right) (top left) An example from MNIST and (bottom right) an example from USPS with a 90° right rotation; (top right) the OT plan T 2 between the rows of MNIST and USPS; (bottom left) the OT plan T 3 between the columns of MNIST and USPS; the arrows explain how to match the pixels between the two datasets using T 2 and T 3 obtained with OTT.
Illustration above:
- (Left) Transport plan T 1 between 400 images (only digits 0 and 1) of MNIST and USPS datasets;
- (Right) (top left) An example from MNIST and (bottom right) an example from USPS with a 90° right rotation; (top right) the OT plan T 2 between the rows of MNIST and USPS; (bottom left) the OT plan T 3 between the columns of MNIST and USPS; the arrows explain how to match the pixels between the two datasets using T 2 and T 3 obtained with OTT.

Proposed stochastic optimization algorithm that drastically reduces the computational complexity of the OTT formulation, making it usable in practice
Illustration above: Proposed stochastic optimization algorithm that drastically reduces the computational complexity of the OTT formulation, making it usable in practice.
Read the full article at : https://hal.archives-ouvertes.fr/hal-03479241/document
Code available at : https://github.com/Hv0nnus/Optimal_Tensor_Transport
Contact : remi.emonet @ univ-st-etienne.fr
The 36th AAAI Conference on Artificial Intelligence is a virtual event that will take place from 22nd February to 1st March 2022 : https://aaai.org/Conferences/AAAI-22/

